Introductions
Understanding camera parameters
Craniofacial Superimposition
Published on November 29, 2019
Written by Andrea Valsecchi
Performing craniofacial superimposition involves superimposing a 3D model of a skull over an ante-mortem photo showing the face of a certain person. The analyst carrying out the task aims to have the skull overlaying the face of the subject by matching its position, pose and size.
This suggests the idea that a superimposition simply involves visualizing and manipulating a 3D model by means of translation, rotation and scaling operations. This is what photo editing software such as Adobe Photoshop provide. However, a closer look at the superimposition process reveals that there is more to it. The appearance of the face in a photo is determined by the way the photo has been acquired.
This involves not just where the camera was placed and what it was aimed at, but also the specific kind of camera, the lens and the camera settings used to take the photo. When performing a superimposition, the analyst is aiming to reproduce the ante-mortem photo by taking a photo of the skull under the same conditions. It this therefore essential to understand what factors are involved in acquiring a photo and what is their effect on the appearance of skull.
These factors are called camera parameters, and they are subject of this article.
The pinhole camera model
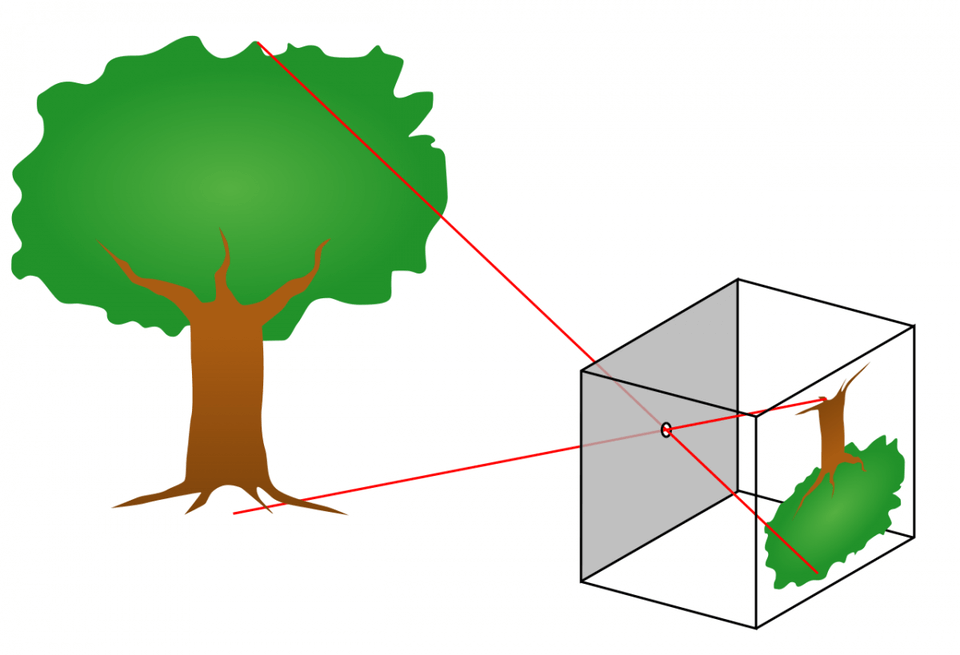
A pinhole camera is an early type of camera where light is focused by a tiny aperture in the front wall. More recent cameras, including modern digital cameras, use lenses instead. Nevertheless, all cameras behave essentially as pinhole cameras, and indeed the mathematical model of a camera is called the pinhole camera model. The model describes how a point of the 3D space being photographed is projected onto the 2D plane of the photo. In other words, the camera model provides a mathematical formula that, given the coordinates of a point of the 3D space, allows to calculate the corresponding coordinates of the point in the photo. While most real cameras do not follow the pinhole camera model exactly, the model is precise enough for applications to CFS.
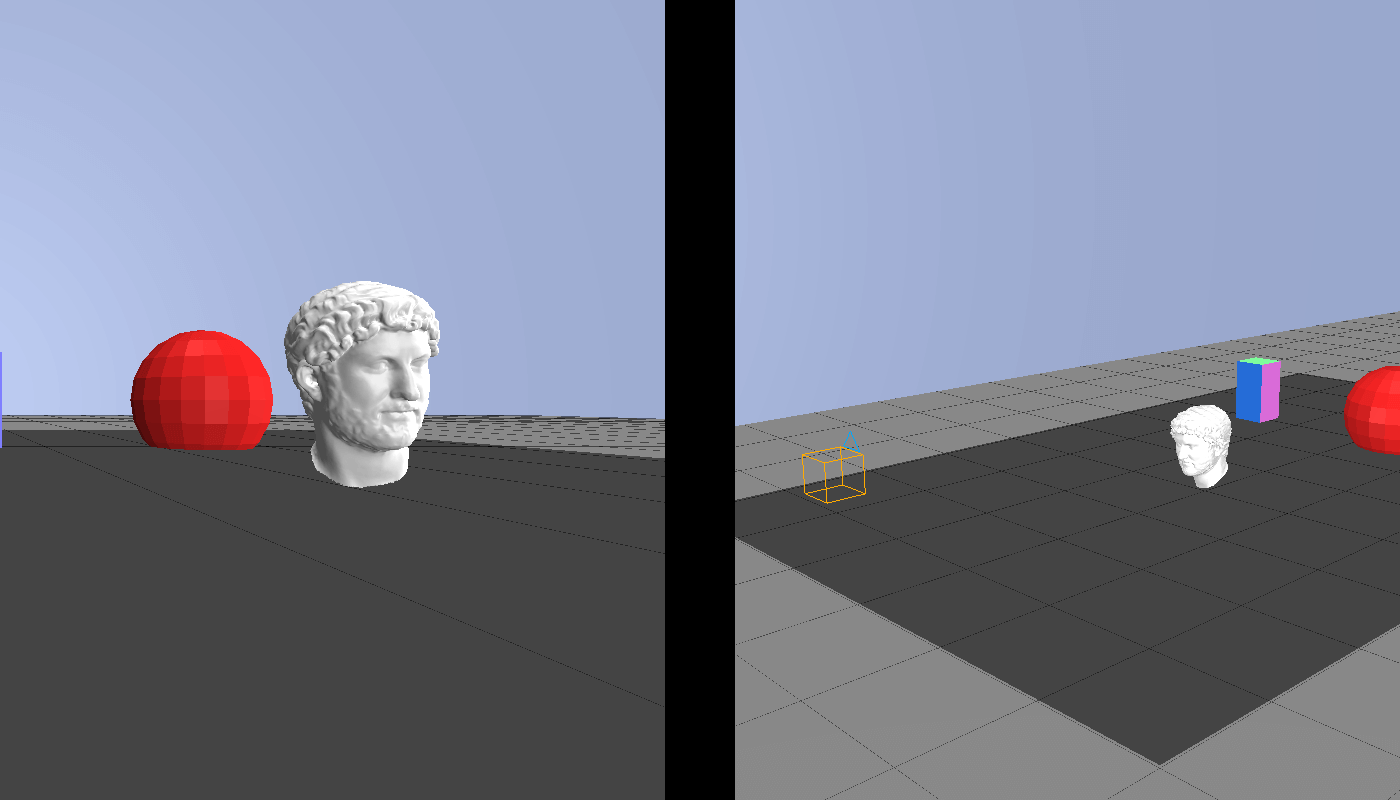
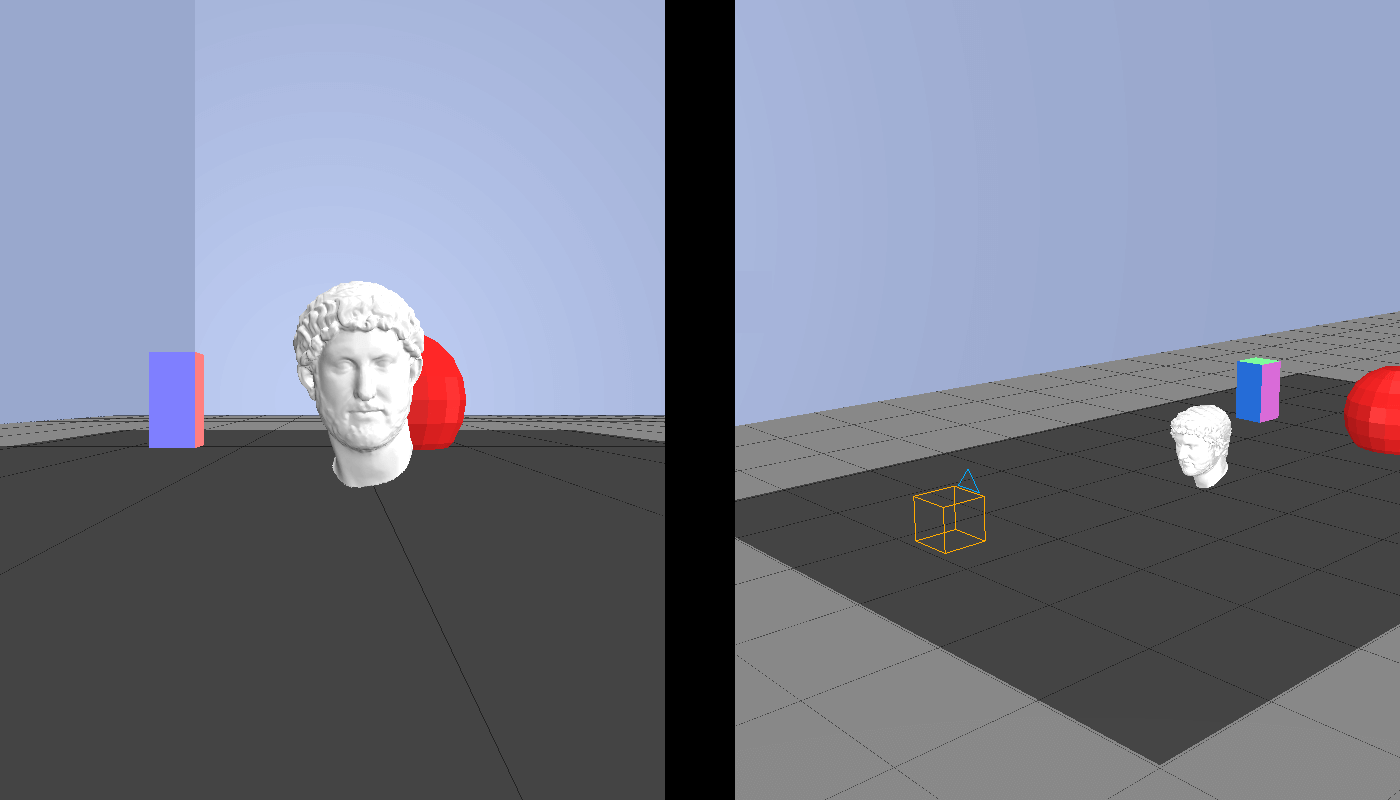
The camera model is what specifies the camera parameters, which are a series of factors that determines how a photo is being taken. Before going further, let us consider an example. A camera has been placed in front of a statue with a colored pillar and red sphere behind it. This scene is depicted in Figure 2, right side; the orange box is the camera. Figure 2, left side shows the actual picture acquired by the camera.

With this scenario in mind, we now introduce the camera parameters and show their effect over the photo.
- Camera position. This is the location of the camera, represented by a point in 3D space.
- Camera orientation. The direction the camera is facing, represented through three angles.
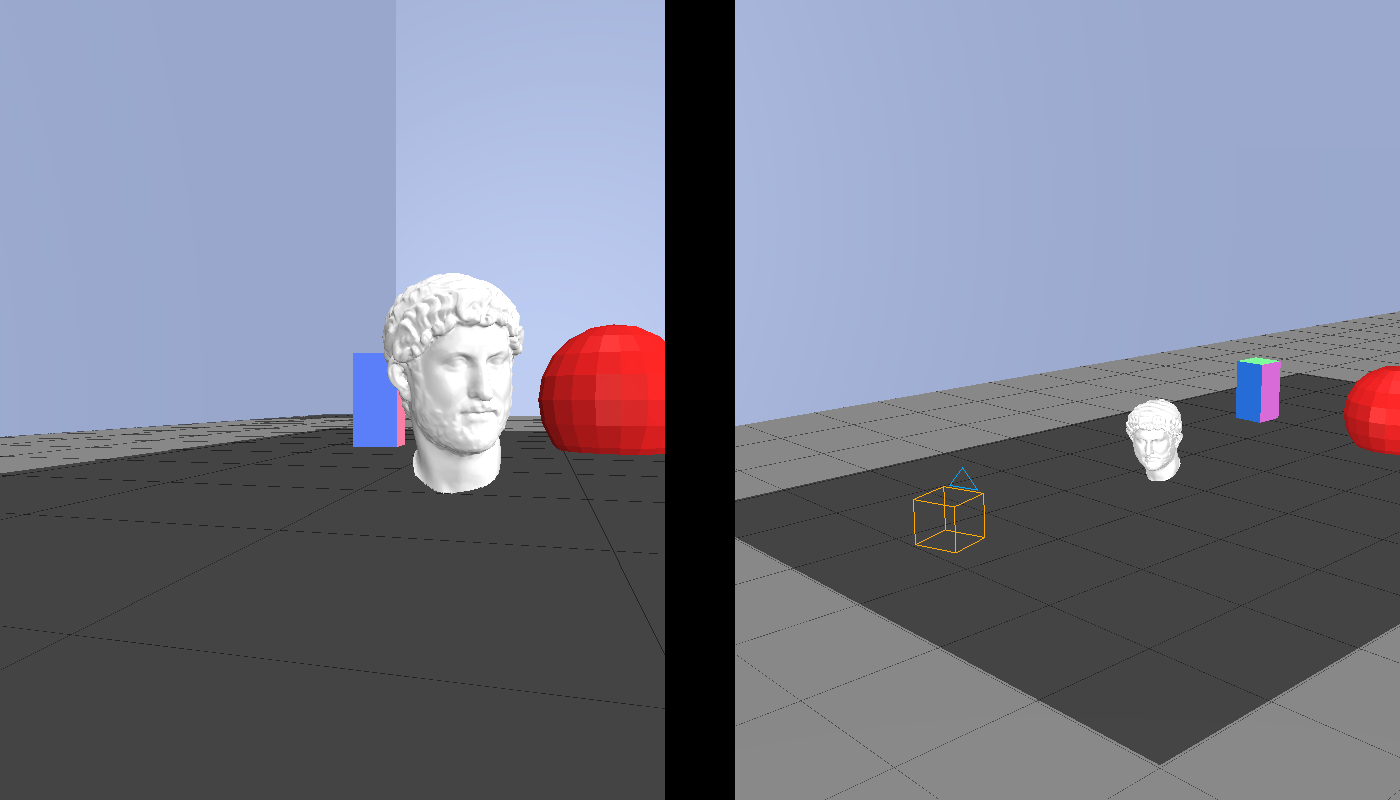
- Focal length. This is a feature of the lens being used; it determines the angle of view of the photo or, loosely speaking, the amount of zoom. Typical values belong to the range 18-300 mm. Small focal length values correspond to wide angle photos and vice-versa. Figure 4 shows four photos of the same scene taken at 35, 70, 100 and 150 mm; notice the camera doesn’t move but the subject gets bigger as the focal length increases. The range of focal length available in a camera depends on the specific lens installed. Often, the focal length value used by a digital camera is recorded with the photo in the EXIF metadata, allowing its value to be set manually.
- Sensor size. This is the physical width of the film or digital sensor that captures the image. It has a similar but opposite effect with respect to focal length, i.e. halving the size of the sensor results in the same photo as doubling the focal length. Most professional camera have a sensor size of 35 mm.
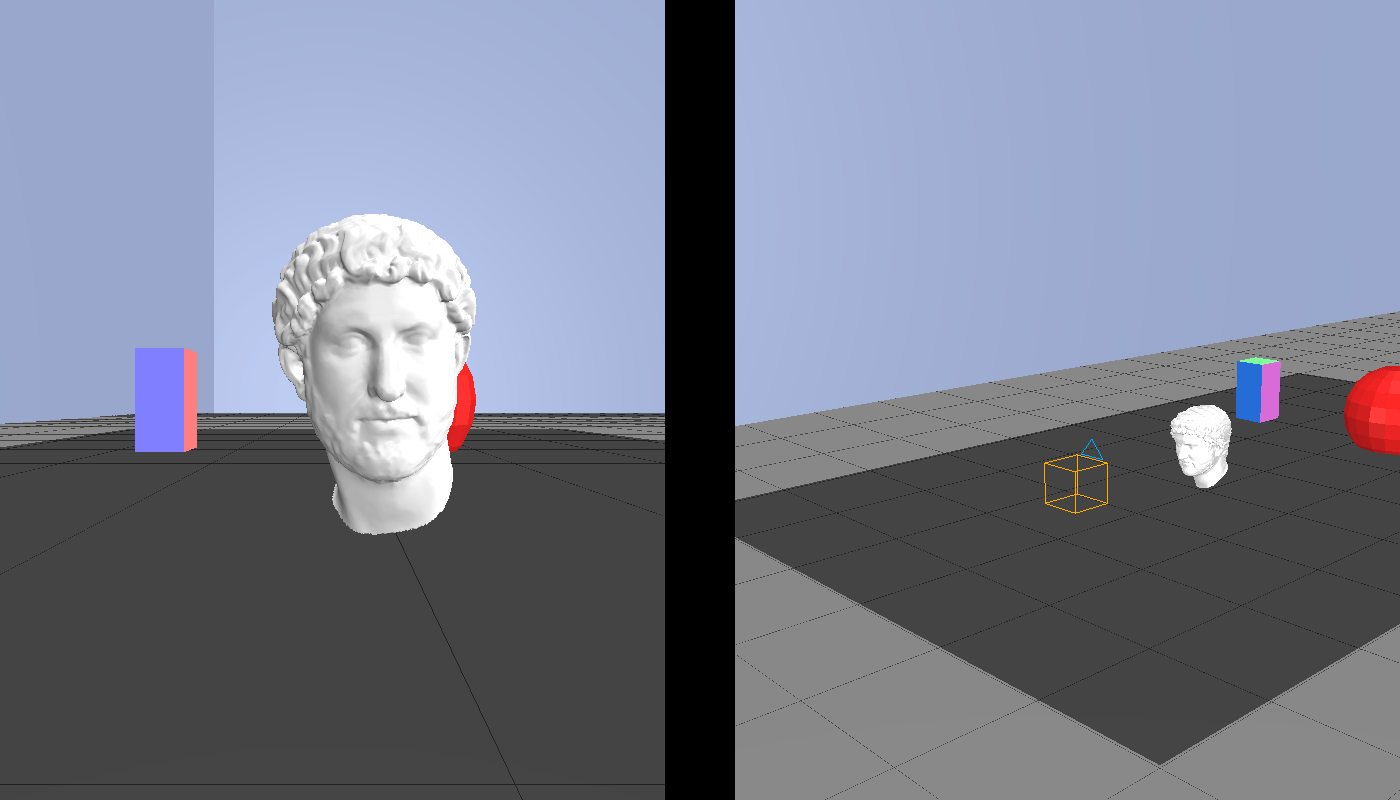
- Subject-to-camera distance (SCD). It is the actual distance between the camera and the subject. Varying the subject-to-camera distance obviously alter the camera position. If the camera gets closer to the subject, the latter appears larger in the photo. However, unlike increasing the focal length, lowering the SCD would result in the subject showing perspective distortion. When the latter occurs, the part of the head being closest to the camera (usually the nose) appears unnaturally large with respect to the rest of the head. The opposite happens to the further parts of the face, e.g. hair and ears.
Figure 5 shows a comparison between a close-up shot and one taken at high focal length. While the apparent size of the head is similar in the two photos, the one with small SCD show noticeable signs of perspective distortion.
- Principal point. The displacement of the principal point is a phenomenon that can be found in wide-angle (small focal length) photos that have been cropped. Consider the following image.

One can notice the subject appears to be stretched horizontally due to perspective distortion. Focusing on the lines on the floor, one can easily recognize the pattern of this distortion: lines that are parallel in the actual scene appear to converge towards the center of the photo. Then, consider this image.

The lines appear to converge, but not towards the center of the photo, rather outside of it. This is a sign that the photo has been cropped. The original image was much wider and had lines converging to the center of it. The principal point is the point where the lines converge; by displacing it one, can reproduce the effect the photo being a portion of a larger photo. When introducing values for the principal point, there is a horizontal and vertical axis, with 0 corresponding to the center, -1 to the leftmost/uppermost point and 1 to the rightmost/lowermost one. The principal point is seldom changed alone, but rather as part of the change parallax operation described in the next section.
Advanced camera operations
This section includes two complex operations, each changing two camera parameters at once with a specific purpose.
- Change perspective. This operation combines a reduction in focal length with a reduction in subject-to-camera distance. The former makes the subject smaller, while the latter makes it bigger. The overall effect is that the apparent size of the subject does not change, but the amount of perspective distortion is increased. These operations allow to change the amount of perspective distortion without changing the apparent size of the subject.
- Change Parallax. This operation combines a displacement of the principal point with a translation of the camera.
While moving the principal point produces a stretching of the subject, it also displaces the subject from its original position.
The camera movement performed in this operation prevents the latter effect, keeping the subject in the same location.